The impetus for this post came from my personal struggles to find a solid reference and working code demonstration of what are called “noise worms”, as I had stumbled upon an illustration and brief description of them when researching some early (2000’s era) procedural generation techniques. The best write up I came across is that given on libnoise from which this post is inspired.

Overview

Noise Worms are a procedurally generated illustrations of worm like objects, which are composed of joined line segments (polylines) orientated by a noise function, Perlin Noise (Perlin & Hoffert, 1989) in our case. An example of a collection of noise worms is given below:

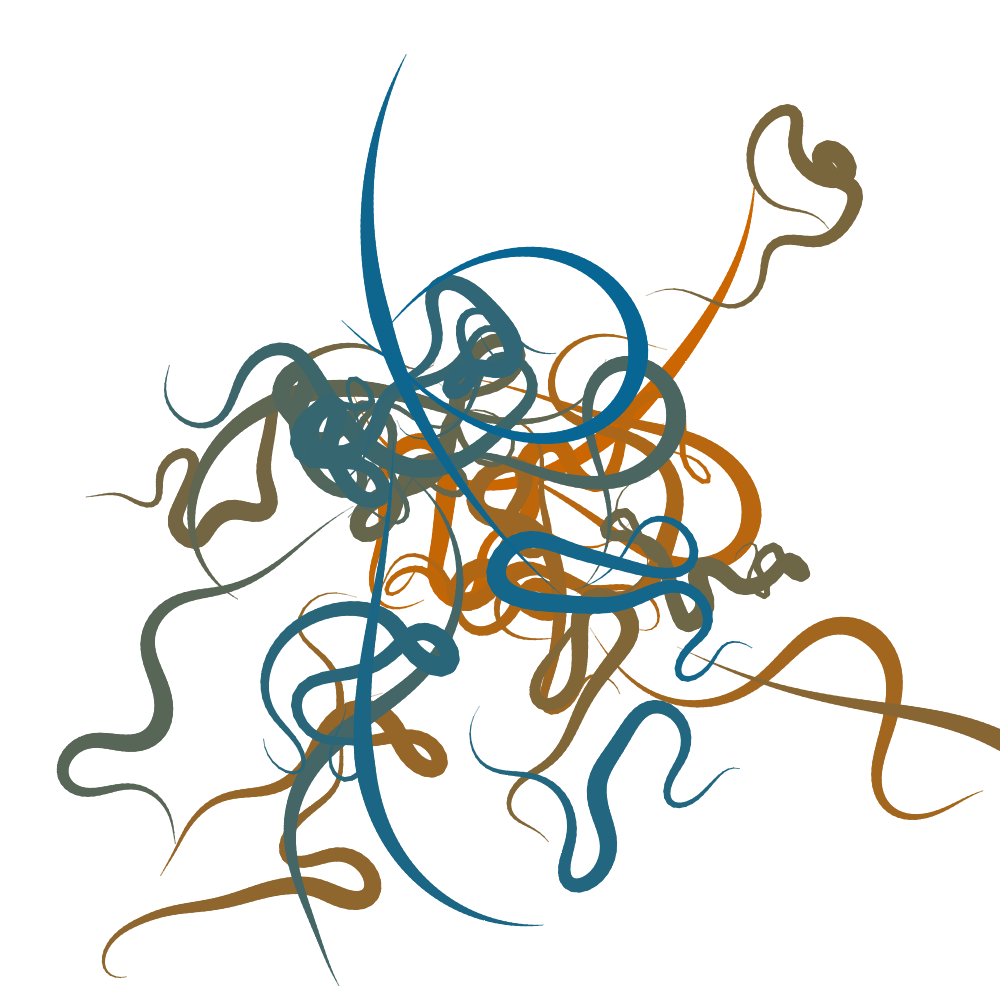
Implementing Perlin noise

Out of historical interest, we will be using a JavaScript port of Perlin’s Improved noise Java reference implementation, given in (Perlin, 2002), which I implemented using the p5.js graphics library.

//Port of Ken Perlin's 2002 Java Reference Implementation of Improved Noise
//to JavaScript

//BUILD PERMUTATION (AND HASH) ARRAY 
let p = []; //LENGTH OF 512
let permutation = [151,160,137,91,90,15, 131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
  190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
  88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
  77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
  102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
  135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
  5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
  223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
  129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
  251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
  49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
  138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180];
for(i=0; i < 256; i++){
  p[256+i] = p[i] = permutation[i]; 
}

function pNoise(x, y, z) {
  let X = Math.floor(x) & 255; // FIND UNIT SQUARE THAT
  let Y = Math.floor(y) & 255; // CONTAINS POINT.
  let Z = Math.floor(z) & 255;
      x -= Math.floor(x);      // FIND RELATIVE X,Y,Z
      y -= Math.floor(y);      // OF POINT IN CUBE.
      z -= Math.floor(z);
  let u = fade(x);             // COMPUTE FADE CURVES
  let v = fade(y);             // FOR EACH OF X,Y.
  let w = fade(z);
  let A = p[X  ]+Y, AA = p[A]+Z, AB = p[A+1]+Z,  // HASH COORDINATES OF
      B = p[X+1]+Y, BA = p[B]+Z, BB = p[B+1]+Z;  // THE 4 SQUARE CORNERS,

  return linerp(w, linerp(v, linerp(u, grad(p[AA  ], x  , y  , z   ),  // AND ADD
                                       grad(p[BA  ], x-1, y  , z   )), // BLENDED
                             linerp(u, grad(p[AB  ], x  , y-1, z   ),  // RESULTS
                                       grad(p[BB  ], x-1, y-1, z   ))),// FROM  8
                   linerp(v, linerp(u, grad(p[AA+1], x  , y  , z-1 ),  // CORNERS
                                       grad(p[BA+1], x-1, y  , z-1 )), // OF CUBE
                             linerp(u, grad(p[AB+1], x  , y-1, z-1 ),
                                       grad(p[BB+1], x-1, y-1, z-1 ))));
}
   
function fade(t) { return t * t * t * (t * (t * 6 - 15) + 10); }
function linerp(t, a, b) { return a + t * (b - a); }
function grad(hash, x, y, z) {
  let h = hash & 15;    // CONVERT LOW 4 BITS OF HASH CODE INTO 12 GRADIENT DIRECTIONS.
  let u = h<8 ? x : y;
  let v = h<4 ? y : h==12||h==14 ? x : z;
  return ((h&1) == 0 ? u : -u) + ((h&2) == 0 ? v : -v);
}

Taking a 2D slice of the 3D noise volume on a uniformly spaced grid (often also called a Lattice) of sample points gives the following image:

function setup(){
  //draw grid of noise values
  createCanvas(80,80);
  background(255);
  
  for(i=0; i<width*height; i++){
    noStroke();
    fill((pNoise(i%width+0.3, ~~(i/height)+0.4, 10)+1)*128);
    square(i%width, ~~(i/height), 2);
  }
}

The sharp contrast between cells (pixels) is due to the coarse sampling of grid points. If we were to sample in a more continual sweep across the space, we would get smooth boundaries due to the spline interpolation used within the algorithm. The following image illustrates this for a finer grid.

function setup(){
  //draw grid of noise values
  createCanvas(80,80);
  background(255);
  
  for(i=0; i<10*width*height; i++){
    for(j=0; j<10; j++){
      noStroke();
      fill((pNoise(i%width+0.1*j, ~~(i/height)/10, 10)+1)*128);
      square(i%width+0.1*j, ~~(i/height)/10, 1);
    }
  }
}

Constructing the worms

Given our noise domain (defined above) we can construct the worms. To do this, a lookup line segment is placed within a noise domain (e.g., Perlin Noise is used here as it gives a coherent space) and used it to perform directional lookups at sample points along its length. These sample points correspond to segments on the worm and are used to orient each relative to the previous segment along the worm.

The following code defines a simple worm class, a sampling segment, and a loop for rendering the worm based on the noise samples drawn from the segment.

class Worm{
  constructor(x,y,c){
    this.x = x;
    this.y = y;
    this.seg = [x,y];
    this.len = this.seg.length;
    this.c = c;
  }
  
  grow(x,y){
    this.seg.push(x,y);
    this.len = this.len + 2;
    this.x = x;
    this.y = y;
  }
  
  display(){
    let girth = Math.min(5,this.len/2);
    //draw the worm segment by segment    
    let i = 1;
    while(i<this.len-2){
      if(i<this.len/2){
        strokeWeight(girth*(2*i/this.len));
      }else{
        strokeWeight(girth*(2*(this.len-i)/this.len));
      }
      stroke(this.c);
      line(this.seg[i-1],this.seg[i],this.seg[i+1],this.seg[i+2]);
      i += 2;
    }
  }
}

function setup(){
  createCanvas(500,500);
  background(255);
  angleMode(RADIANS);
  
  let w = new Worm(random(150,350),random(150,350),'#967445'); 
  let lsegXmax = random(10,240);
  let lsegX = (lsegXmax-10)/maxLen;
  let lsegY = random(0,255);
  
  for(i=0; i<30; i++){
    let segLen = random(5,20);
    let pN = pNoise(lsegX*i,lsegY,1);
    let dx = segLen*cos(PI*(pN+1));
    let dy = segLen*sin(PI*(pN+1));
    if(w.x+dx < 0 || w.x+dx > width){  //boundary detection
      dx = -dx;
    }
    if(w.y+dy < 0 || w.y+dy > height){
      dy = -dy;
    }
    w.grow(w.x+dx,w.y+dy);  //add segment to worm
  }
  w.display();
}

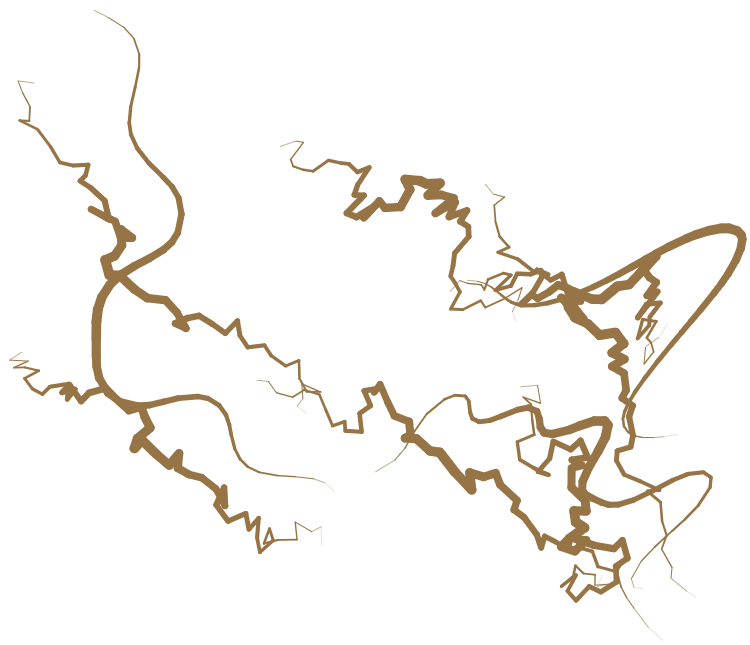
Here are two examples for the kinds of worms that can be generated using this simple script and method for two different randomly placed segments within the same noise volume. The worm that turns smoothly, that is does not jitter, results from a finely divided lookup segment in the noise domain, and vise versa for the worm with lots of jitter.

As can be seen, generating procedural objects like these is incredibly simple and the method achieves a good amount of diversity in generation.

This method, which is quite bear bones, can be further modified to generate worms with directional bias to give increasingly varied results.

function setup(){
  createCanvas(500,500);
  angleMode(RADIANS);
  
  let nWorms = 10;
  let maxLen = 50;
  
  //create array of worms
  for(n=0; n<nWorms; n++){
    let w = new Worm(random(150,350),random(150,350),'#967445'); 
    let lsegXstart = random(10,240);
    let lsegXend = random(lsegXstart,lsegXstart+10);
    let lsegX = (lsegXend-lsegXstart)/maxLen;
    let lsegY = random(0,255);
    let lsegZ = random(1,255);
    let xBias = random(1,1.5);
    let yBias = random(1,1.5);
    for(i=0; i<maxLen; i++){
      let segLen = random(5,10);
      let pN = pNoise(lsegX*i,lsegY,lsegZ);
      let dx = segLen*cos(xBias*PI*(pN+1));
      let dy = segLen*sin(yBias*PI*(pN+1));
      if(w.x+dx < 0 || w.x+dx > width){  //boundary detection
        dx = -dx;
      }
      if(w.y+dy < 0 || w.y+dy > height){
        dy = -dy;
      }
      w.grow(w.x+dx,w.y+dy);  //add segment to worm
    }
    w.display();
  }
}

By implementing different distance bias expressions for \(dx\) and \(dy\), respectively the displacement in \(x\) and \(y\), a wide range of different appearances can be achieved.

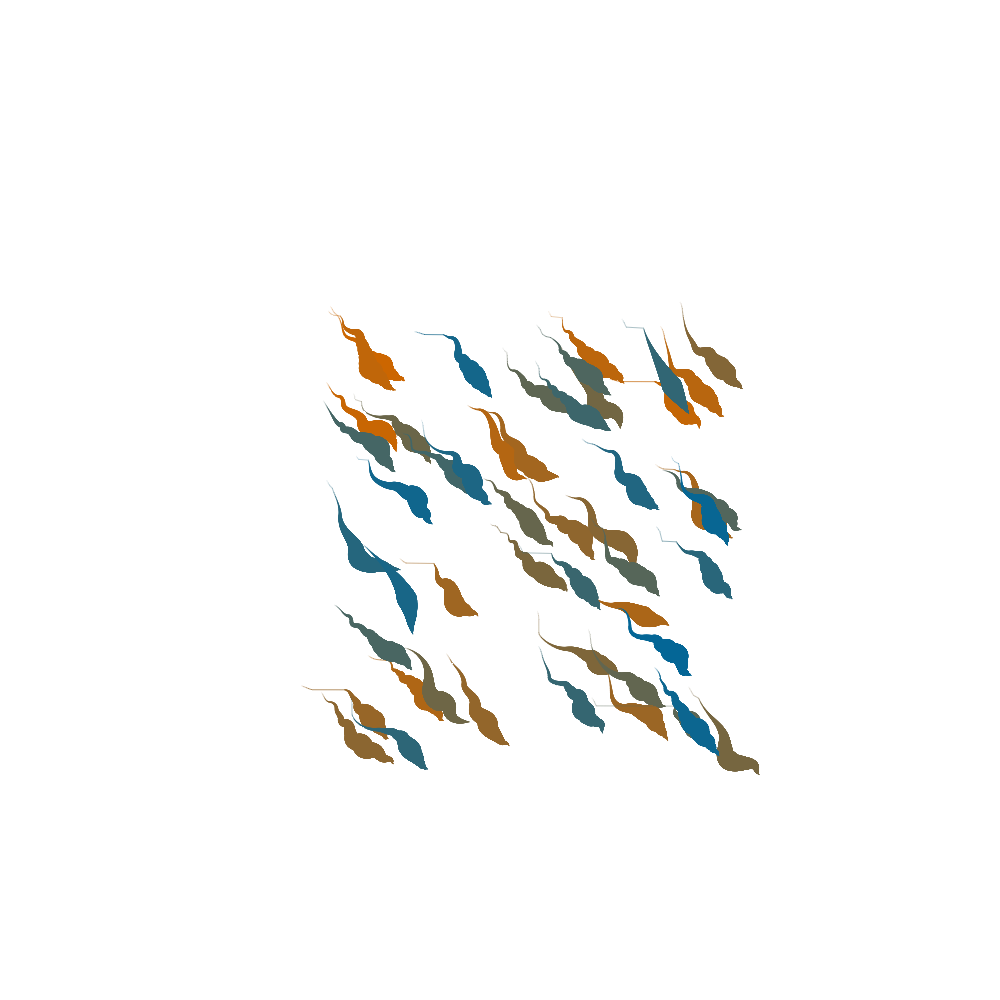
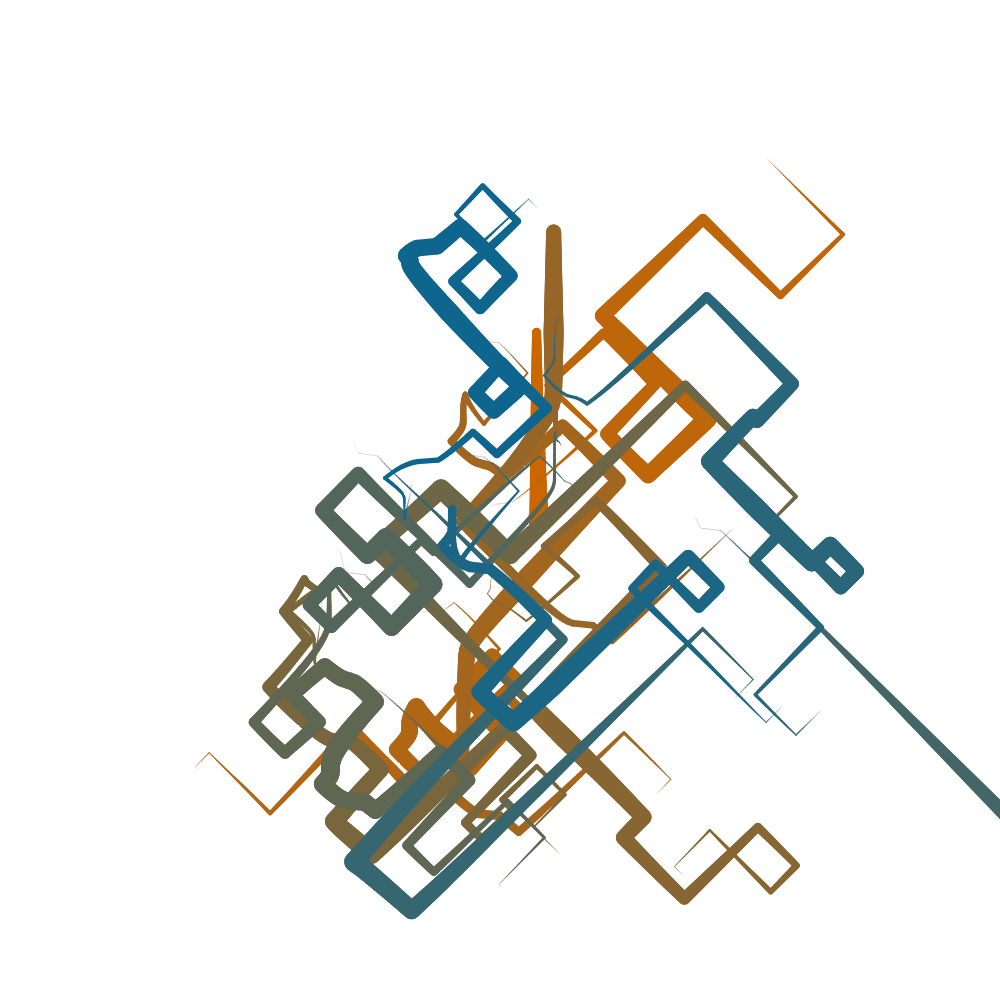
Animating the worms

Due to Perlin noise being a source of coherent noise, meaning its output changes smoothly and proportionately with small and large changes in input, worms can be smoothly animated by gradually translating their lookup segments within the noise domain and accordingly updating segments along the worms.

The following code animates a singular worm using the simple method proposed above.

let nWorms = 10;    // number of worms
let maxLen = 30;    // number of segments on a worm 
let worms = [];     // array of worms
let segMaxLen = 10; // lookup segment max length
let segs  = [];     // array of lookup segments [..., x, y, z, div, xBias, yBias, ...]
let dirVec = [];    // array of direction vectors for lookup segment translation


function setup(){
  createCanvas(500,500);  //set up window
  angleMode(RADIANS);
  
  //create array of worms
  for(n=0; n<nWorms; n++){
    worms[n] = new Worm(random(150,350),random(150,350),'#967445'); 
    segs[n*6  ] = random(10,240);
    segs[n*6+1] = random(1,255);
    segs[n*6+2] = random(1,255);
    segs[n*6+3] = (random(segs[n*5],segs[n*5]+segMaxLen)-segs[n*5])/maxLen;
    segs[n*6+4] = random(1,1.5);
    segs[n*6+5] = random(1,1.5);
    for(i=0; i<maxLen; i++){
      let segLen = 5; //random(5,10);
      let pN = pNoise(segs[n*6]+segs[n*6+3]*i,segs[n*6+1],segs[n*6+2]);
      let dx = segLen*cos(segs[n*6+4]*PI*(pN+1));
      let dy = segLen*sin(segs[n*6+5]*PI*(pN+1));
      if(worms[n].x+dx < 0 || worms[n].x+dx > width){  //boundary detection
        dx = -dx;
      }
      if(worms[n].y+dy < 0 || worms[n].y+dy > height){
        dy = -dy;
      }
      worms[n].grow(worms[n].x+dx,worms[n].y+dy);  //add segment to worm
    }
    worms[n].display();
  }
}

function draw(){
  frameRate(30);
  clear();
  
  for(n=0; n<nWorms; n++){
    let dirX = 0.05;
    let dirY = 0;
    let dirZ = 0.01;
    
    segs[n*6  ] += dirX;
    segs[n*6+1] += dirY;
    segs[n*6+2] += dirZ;
    
    let i = 0;
    while(i<worms[n].len){
      let segLen = 5;
      let pN = pNoise(segs[n*6]+segs[n*6+3]*i,segs[n*6+1],segs[n*6+2]);
      if(i==0){
        let dx = cos(segs[n*6+4]*PI*(pN+1));
        let dy = sin(segs[n*6+5]*PI*(pN+1));
        if(worms[n].seg[i]+dx < 0 || worms[n].seg[i]+dx > width){  //boundary detection
          dx = -dx;
        }
        if(worms[n].seg[i+1]+dy < 0 || worms[n].seg[i+1]+dy > height){
          dy = -dy;
        }
        worms[n].seg[i  ] += dx;
        worms[n].seg[i+1] += dy; 
      }else{
        //segLen = dist(worms[n].seg[2*i-2],worms[n].seg[2*i-1],worms[n].seg[2*i],worms[n].seg[2*i+1]);
        let dx = segLen*cos(segs[n*6+4]*PI*(pN+1));
        let dy = segLen*sin(segs[n*6+5]*PI*(pN+1));
        if(worms[n].seg[2*i-2]+dx < 0 || worms[n].seg[2*i-2]+dx > width){  //boundary detection
          dx = -dx;
        }
        if(worms[n].seg[2*i-1]+dy < 0 || worms[n].seg[2*i-1]+dy > height){
          dy = -dy;
        }
        worms[n].seg[2*i  ] = worms[n].seg[2*i-2]+dx;
        worms[n].seg[2*i+1] = worms[n].seg[2*i-1]+dy; 
      }
      i += 1;
    }
    worms[n].display();
  }
}

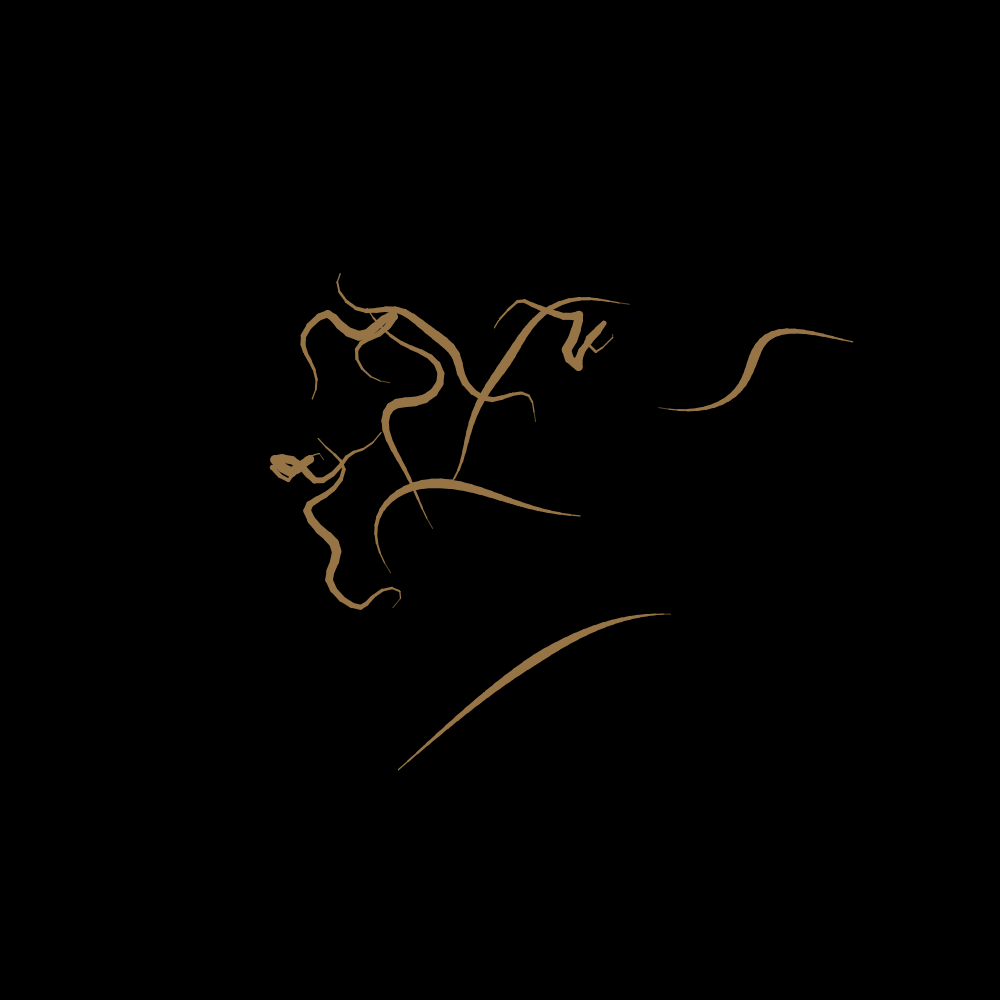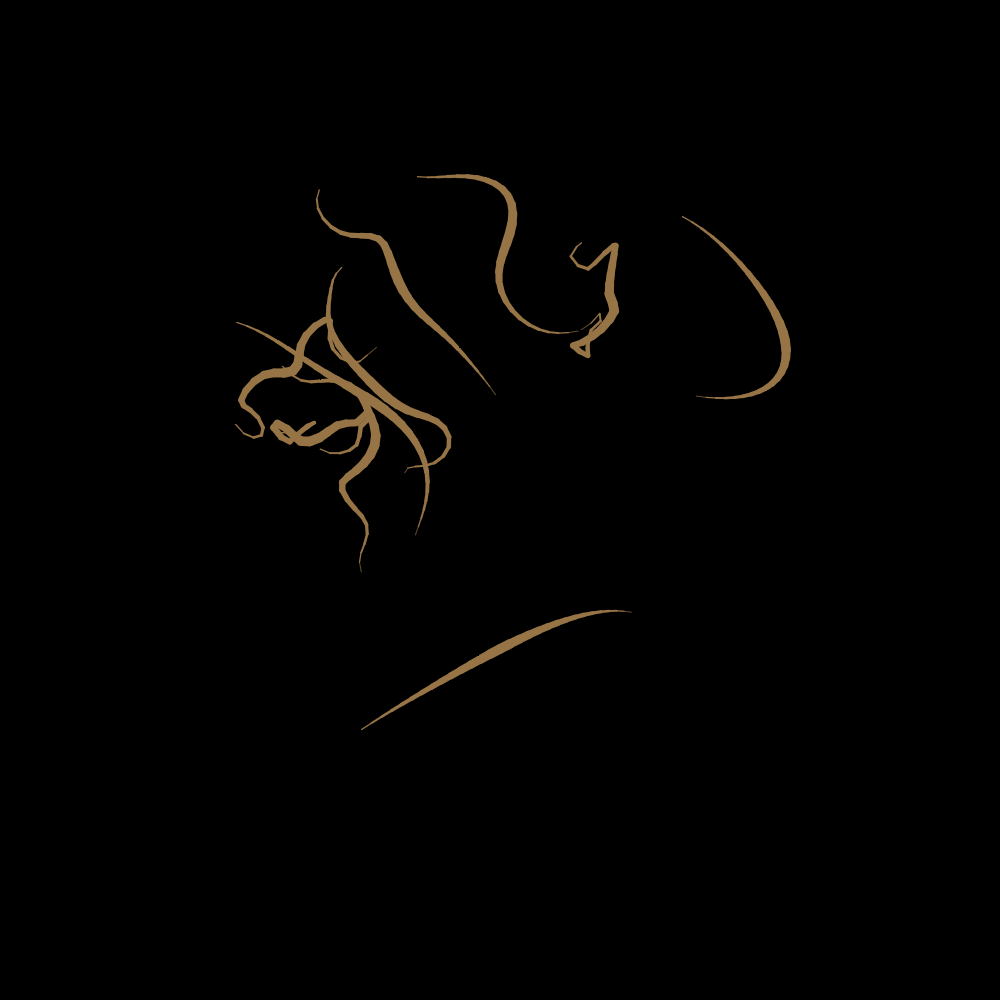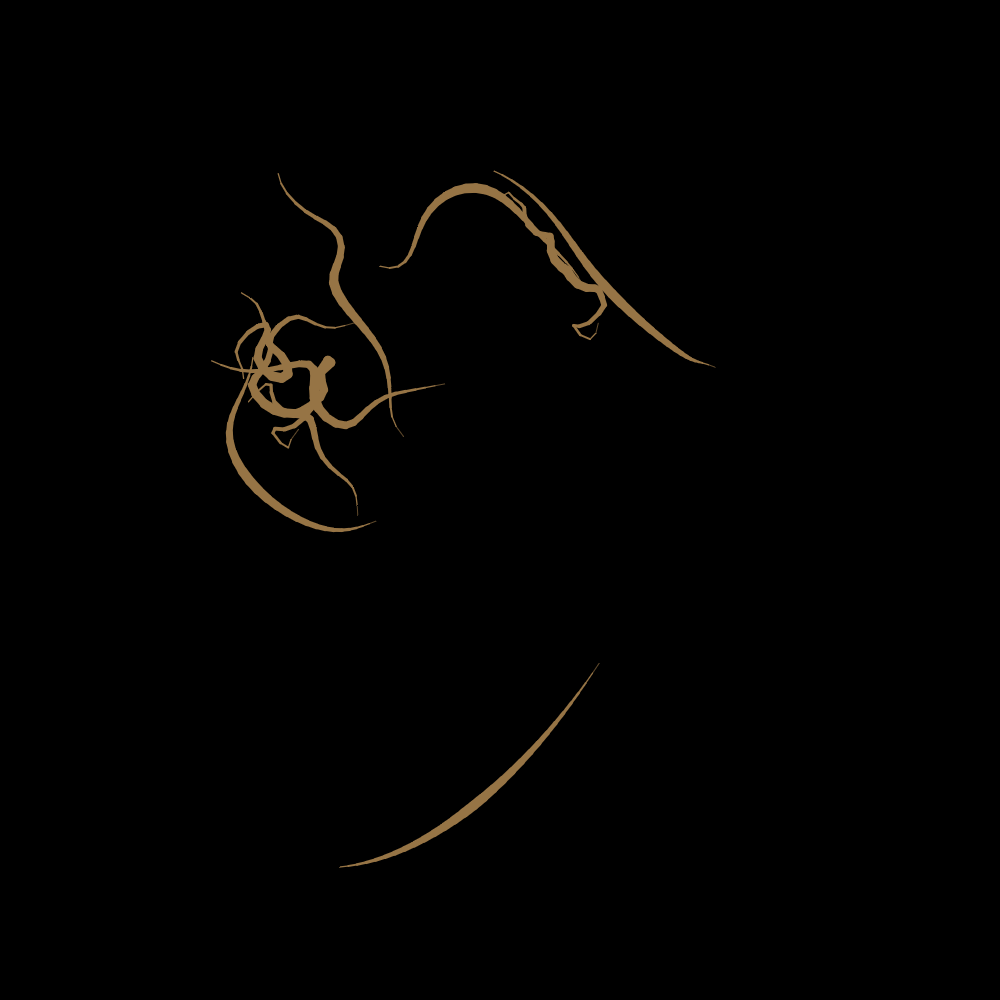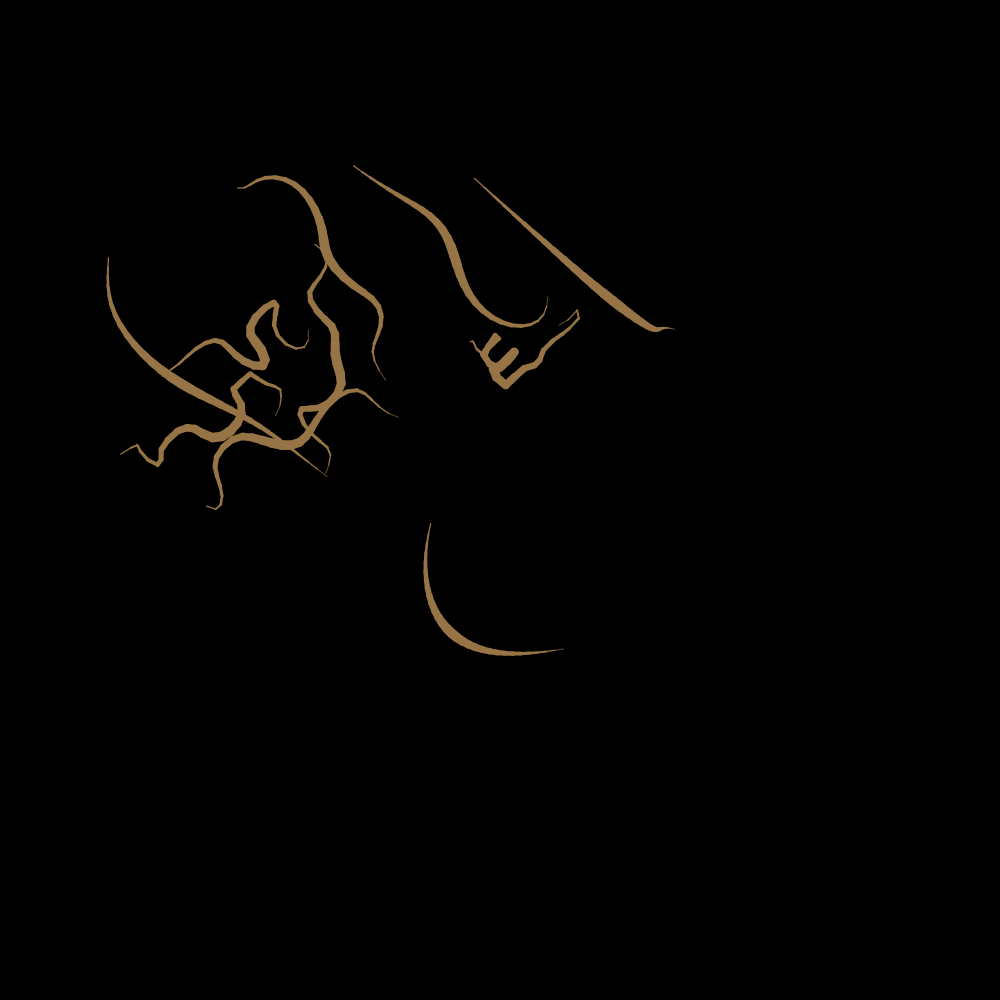
Disgusting.

Animating other objects using noise

This method of pseudo-random animation is not limited to line segments but can be applied to any set of vertices by associating each to a moving point in the noise domain.

We model phenomena intermediate between shape and texture by using space-filling applicative functions to modulate density. The model is essentially an extension of procedural solid texture synthesis, but evaluated throughout a volumetric region instead of only at surfaces.We have been able to obtain visually realistic representations of such shape+texture (hypertexture) phenomena as hair, fur, fire, glass, fluid flow and erosion effects. We show how this is done, first by describing a set of base level functions to provide basic texture and control capability, then by combining these to synthesize various phenomena.Hypertexture exists within an intermediate region between object and not-object. We introduce a notion of generalized boolean shape operators to combine shapes having such a region.Rendering is accomplished by ray marching from the eye point through the volume to accumulate opacity along each ray. We have implemented our hypertexture rendering algorithms on a traditional serial computer, a distributed network of computers and a coarse-grain MIMD computer. Extensions to the rendering technique incorporating refraction and reflection effects are discussed.

Perlin Worms

Overview

Implementing Perlin noise

Constructing the worms

Animating the worms

Animating other objects using noise

References

2002

1989

Enjoy Reading This Article?